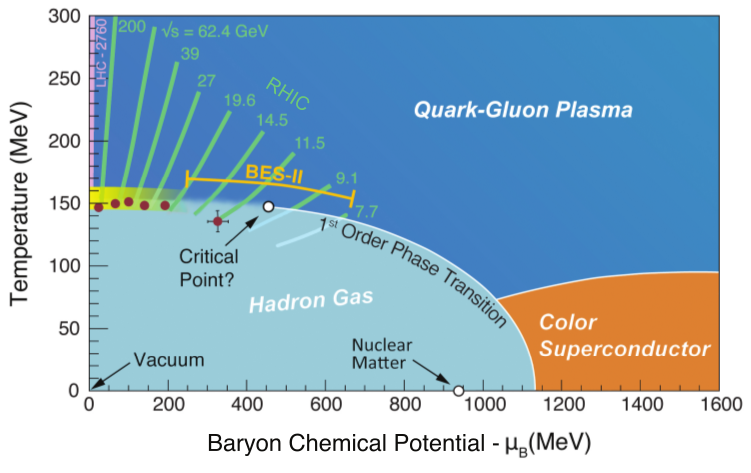
Lattice QCD calculations at non-zero temperature and baryon
chemical potential allow the exploration of the transition and crossover lines
separating the low temperature hadronic phase from the quark-gluon plasma
phase. They also allow the quantification of the relation between the experimentally
measured freeze-out curve and the crossover
transition line (red circles in the figure,
arXiv:1208.1220 [hep-lat]).
The phase diagram is taken from the
NSAC 2015 Long Range Plan for Nuclear Physics.
At low temperatures and densities ordinary hadrons are the prevailing
degrees of freedom that determine the properties of nuclear matter.
However, under extreme conditions of high temperature or of high density
(or both) this is expected to change. The theory of strong interactions
(Quantum Chromodynamics (QCD)) predicts that a phase transition or
crossover occurs that separates the low temperature/density regime
of ordinary hadronic matter from a high temperature/density region where
quarks and gluons, the basic constituents of QCD, become the most relevant
degrees of freedom.
Deriving detailed predictions for the properties of matter at high temperature
and density directly from QCD is paramount in shaping our understanding of
nuclear matter in general, as well as for understanding the evolution of the
early universe. Large experimental programs at the Relativistic Heavy Ion
Collider (RHIC) at Brookhaven, USA, and the Large Hadron Collider (LHC) in
Geneva, Switzerland, exist which explore the properties of matter at high
temperature and/or density, with the aim of mapping the boundaries between
different phases of strongly interacting matter, and determining
quantitatively the properties of matter in this domain. At RHIC a dedicated
research program, the Beam Energy Scan Program (BES), has been established
that searches for signatures for the existence of a critical point in the
phase diagram that marks the starting point for a line of first order
phase transitions. This is illustrated
in the phase diagram displayed to the right.
Lattice QCD foster this search through calculations of the equation
of state of hot and dense matter, the calculation of conserved charge
fluctuations as well as predictions for the modification of hadron masses,
in particular the heavy quarkonium bound states, in strong interaction
matter.
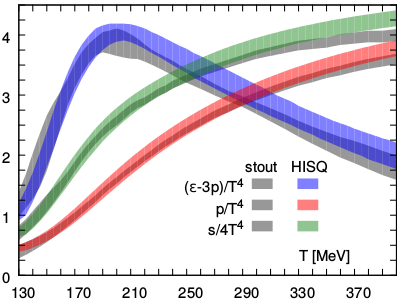
The energy density minus three times the pressure, the pressure
and entropy density of hot strongly interacting matter
divided by appropriate powers of the temperature. These bulk thermodynamic
observables have now been calculated with two different lattice
discretisation schemes (stout and HISQ) and have been extrapolated
to the continuum limit
(arXiv:1407.6387 [hep-lat]).
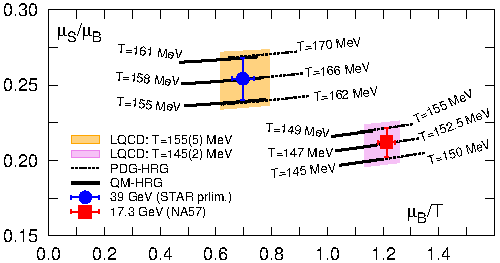
The ratio of strangeness and baryon number chemical potentials
needed to reproduce the production of multiple strange
baryons measured by STAR in the RHIC beam energy scan and
by NA57 at the SPS (CERN) at two different values
of the colliding beam energies. This also fixes the
temperature (T) at which these baryon got produced.
For details see
(arXiv:1404.6511 [hep-lat]).
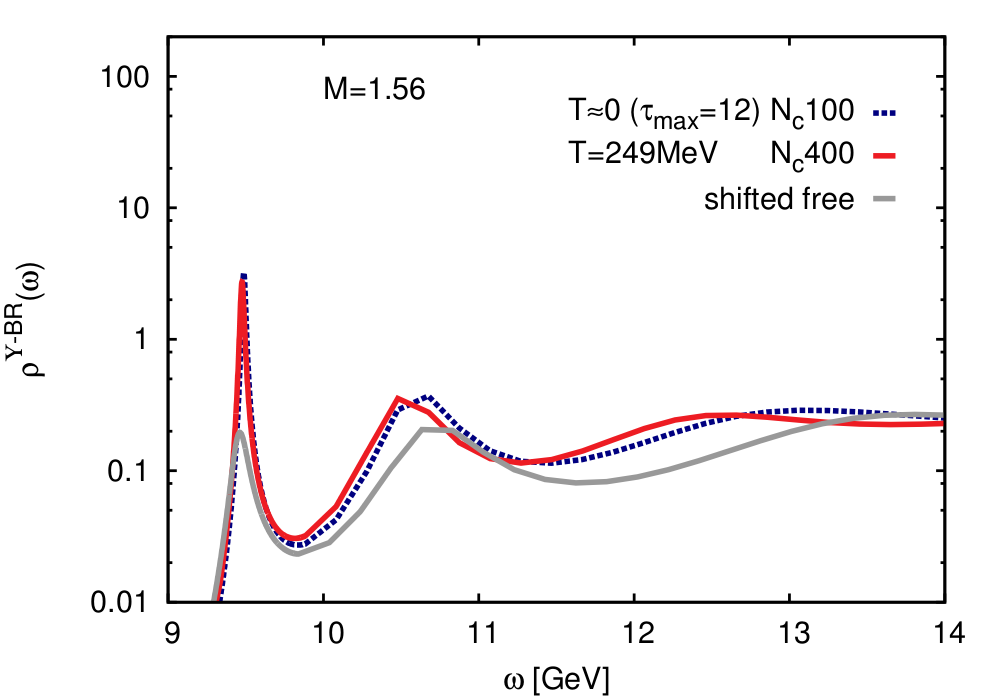
Bottomonium spectral functions reconstructed
from the NRQCD lattice calculations on lattices with temporal extent Nt=12
using a novel Bayesian approach.
Shown are the spectral functions at T=249 MeV and T=0 as well as
the Bayesian reconstruction of the free spectral function that does not
have bound state peaks (Seyong Kim, Peter Petreczky, Alexander Rothkopf, Phys. Rev. D 91, 054511 (2015) ).
For details see
(arXiv:1409.3630 [hep-lat]).
Bulk thermodynamics:
The behavior of strongly interacting matter in the vicinity of the phase
transition or crossover is inherently a strong coupling problem, which can
only be studied from first principles through lattice gauge theory calculations.
Among the issues that can uniquely be addressed by lattice calculations are
the nature of the transition, the temperature at which it occurs, the equation
of state and various properties of the plasma that characterize its
non-perturbative structure. Indeed, numerical calculations that are
performed within the lattice regularized version of QCD have
given us the best estimates of the temperature of the transition from
hadronic matter to the quark-gluon plasma. Properties
of this transition, the transition temperature, its bulk properties
like the equation of state or the velocity of sound in hot and dense
matter are studied extensively using computing resources on leadership
class computers as well as on clusters operated by USQCD at Jefferson
Laboratory and Fermilab. This leads to
a determination of the transition temperature
Tc=154(9) MeV,
and calculations of the
equation of state,
the velocity of sound
that characterizes the expansion of dense matter formed in heavy ion
experiments, and several other properties of this new form of matter.
The upper figure on the left shows
the energy density minus three times the pressure,
which is a measure for deviations from a non-interacting thermal medium.
Also shown are the pressure and entropy density of strongly interacting
matter as a function of temperature for zero net baryon number density.
Continuum extrapolated results are shown for two different discretizations
schemes labeled 'stout' and 'HISQ'.
Fluctuations of conserved charges:
A fundamental set of experimental observables that are being analyzed in
the Beam Energy Scan at RHIC are fluctuations of conserved charges
(baryon number, electric charge, strangeness) and their higher order
cumulants. These are considered to provide unique signatures for
a possible critical point in the QCD phase diagram.
Lattice QCD calculations of cumulants of conserved charge
fluctuations allow to pin down the freeze-out conditions, i.e. the
thermal parameters at the time hadrons form again in the sufficiently cooled
down strongly interacting medium of quarks and gluons.
Calculations of these observables are computationally
demanding. State-of-the-art results have been
obtained on the USQCD and DOE operated GPU cluster at Jefferson National
Laboratory, Fermilab and the BlueGene/Q at BNL. Substantial resources
for these calculations also come from an INCITE grant received by
USQCD that provides access to leadership class computers at Oak Ridge (Titan)
and Argonne (BlueGene/Q).
The middle figure on the left shows results from a
calculation of quadratic fluctuations of net baryon number, electric
charge and strangeness as well as their cross-correlations. These
observables allow to calculated the ratio of strangeness and baryon
chemical potential that is needed to describe a strangeness neutral
system at any value of the temperature. Comparing with experimental
data on particle yields allows to determine the thermal parameters
required for the production (freeze-out) of strange baryons in
ultra-relativistic heavy ion collisions.
Thermal modification of heavy quark bound states:
The suppression of quarkonium yield in heavy ion collisions relative to the scaled proton-proton
collisions was proposed by Matsui and Satz as a signature of the formation of deconfined medium.
The basic idea behind this proposal is that due to the color electric screening the
interaction between the heavy quark and anti-quark becomes short range and the formation
of heavy quark bound states will become impossible for sufficiently high temperature.
Studying quarkonium production in heavy ion collisions is a large part of the experimental
program at RHIC and LHC and the interpretation of the experimental results hinges
on the knowledge of quarkonium dissociation temperatures or more
generally on their properties at non-zero temperature.
The in-medium properties of quarkonia and/or their dissolution is encoded in the
spectral functions. Heavy quark bound states appear as peaks in the spectral function.
Absence of any peak structure indicate dissolution of quarkonium states.
To determine quarkonium spectral functions one has to calculate current-current
correlators on the lattice and find the spectral function by inverse Laplace transform
using Bayesian methods. For heavy quarks this is done in the framework
of non-relativistic QCD (NRQCD).
Using gauge configurations generated during the calculations
of the QCD equation of state, bottomonium correlators and spectral functions have been calculated.
The Upsilon spectral function calculated at a temperature
of about 1.5 times the transition temperature to the high temperature
quark-gluon plasma phase, T=249 MeV, is shown in the bottom figure on the left.
|

